Shopping Cart

No products in the basket.

Shopping Cart

No products in the basket.

Primary 3 More than/Less than & Model Method

Math Heuristics for Problem Solving

Primary 3 More than/Less than & Model Method

What is More than/Less than in Math?

More than/Less than is a type of word problem where we compare two quantities and see which one is bigger or smaller. For example, if we have two people, one who is taller than the other, or if we have two objects, one which is heavier than the other. Key phrases such as ‘than’ are often used to indicate comparison. To solve word problems involving More than/Less than, it can be helpful for primary 3 children to use model drawing to visualize and simplify the problem. The Comparison model method is a good approach to use in this situation.

How to Solve More than/Less than Questions with Comparison Model Method?

Let's take a look at this Primary 3 word problem example:

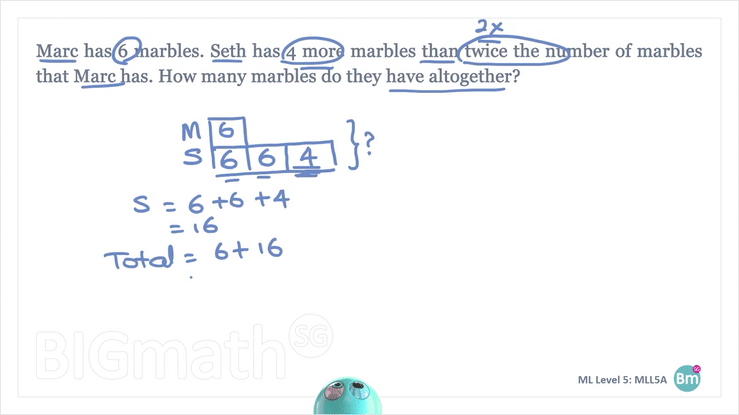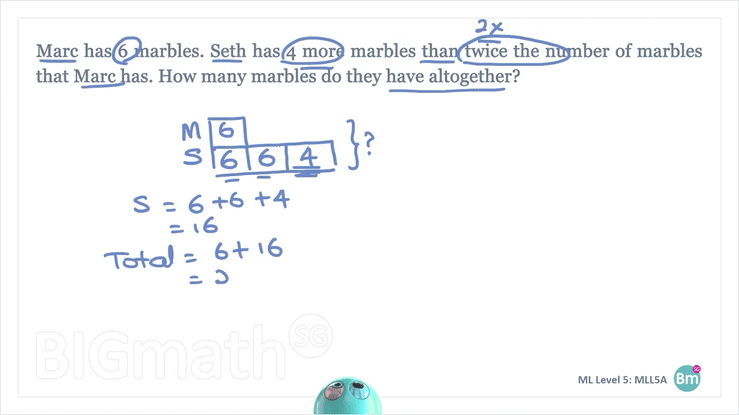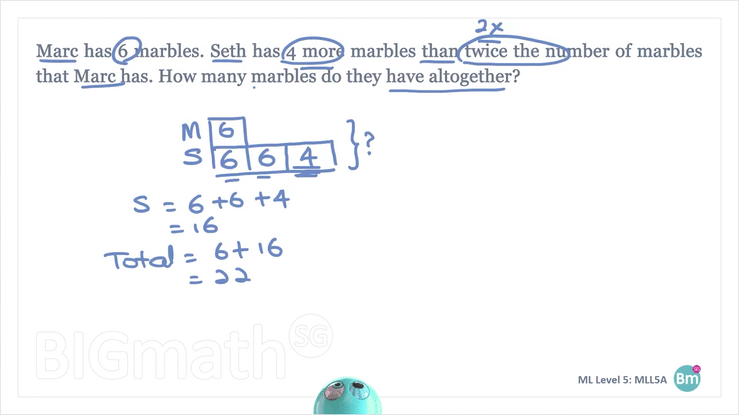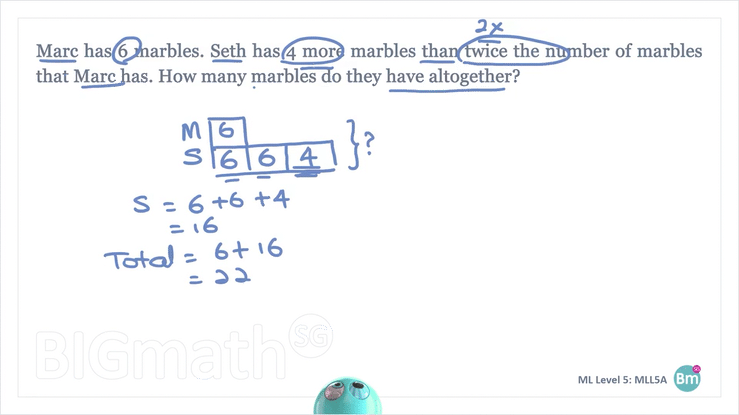
More Than/Less Than Solution
Sign up now!

Watch the tutorial for free!

Marc has 6 marbles. Seth has 4 more marbles than twice the number of marbles that Marc has. How many marbles do they have altogether?

Identify the Concept

2nd sentence tell us this is a More than/Less than concept question as they are comparing the number of marbles between Seth and Marc.

Workings Explained

The 2nd sentence tells us Seth has more marbles than Marc. Therefore we must draw Seth’s model longer than Marc’s model.

  1. Draw Marc’s model, label the model “M”, write “6” in the box as “Marc has 6 marbles”.

  2. Draw 2 parts of Seth’s model the same size as Marc’s model as Seth has “twice the number of marbles Marc has”. Twice means 2 times / 2 groups of the same amount. Write “6” in both the boxes. Draw another box for Seth and write “4” in the box as “Seth has 4 more marbles than twice …”. “Seth has 4 more marbles than twice…” means 2 groups + another 4 more of the amount of marbles Marc has. Label the model “S” for Seth.

  3. The question asks for the total number of marbles both Marc and Seth have. To find the total, we must first find the number of marbles Seth has. Add all the 3 numbers in Seth’s model (6+6+4=16). To find the total, we need to add the number of marbles Marc has and the number of marbles Seth has (6+16=22).

They have 22 marbles altogether.

Can the Comparison Model Method be used to solve other types of word problems?

The Comparison model method can be applied to solve various types of word problems. Some examples of word problem types that can be solved using the Comparison model method include,

See other problem-solving strategies and methods

Watch 13 Math Problem-Solving Lessons for Free!

Simply sign up for Basic Access to get started.

Let's start!

What's Problem Sum?

Problem Sum is a term commonly used in the context of math education, particularly in regions that follow the Singapore Math curriculum. It refers to a type of math problem that typically involves multiple steps and requires students to apply various mathematical concepts and strategies to find the solution. These problems are often word problems that describe a real-world scenario, requiring students to read, comprehend, and analyze the situation before applying the appropriate math operations to solve it.

In essence, a Problem Sum combines elements of arithmetic and logical reasoning, challenging students to think critically and use their problem-solving skills. It is a key component in developing a deeper understanding of math concepts and enhancing analytical abilities in students.